- Joined
- 8/23/24
- Messages
- 4
- Points
- 1
Hello everyone,
I am currently working on pricing an Asian option using the ADI (Alternating Direction Implicit) method, following the guidelines from this article: https://onlinelibrary.wiley.com/doi/10.1155/2013/605943.
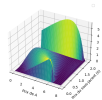
I have been trying for several days to get this right, and despite my efforts, I have not achieved any conclusive results. It seems that I have adhered to the protocol described, including the boundary conditions, and I believe the ADI method is correctly implemented. However, the result I am obtaining is drastically different from what I expected. I have attached the graph I obtained in 3D and the graph I should have obtained for comparison.
Has anyone used this method for pricing options and could offer some guidance or insights?
A = np.linspace(0,K*Tmax,M+1)
S = np.linspace(0,X,N+1)
X, Y = np.meshgrid(S, A)
V = pricing_test_end(sigma=0.4, r=0.06, Tmax=1, K=2, N=30,M=30, E=10, X=8 ,t=0.5,Amax=6)[5][:][:]
ax = plt.axes(projection='3d')
ax.plot_surface(X,Y, V,cmap='viridis')
# Nommer les axes
ax.set_xlabel('Prix de A')
ax.set_ylabel('Prix du sous-jacent (S)')
ax.set_zlabel('Prix de l\'option (V)')
plt.legend()
Thanks,
I am currently working on pricing an Asian option using the ADI (Alternating Direction Implicit) method, following the guidelines from this article: https://onlinelibrary.wiley.com/doi/10.1155/2013/605943.
I have been trying for several days to get this right, and despite my efforts, I have not achieved any conclusive results. It seems that I have adhered to the protocol described, including the boundary conditions, and I believe the ADI method is correctly implemented. However, the result I am obtaining is drastically different from what I expected. I have attached the graph I obtained in 3D and the graph I should have obtained for comparison.
Has anyone used this method for pricing options and could offer some guidance or insights?
def thomas_algorithm(a, b, c, d):
"""
ax_{i-1} + bx_i + cx_{i+1} = d via l'algorithme de Thomas.
"""
n = len(d)
c_prime = np.zeros(n-1)
d_prime = np.zeros(n)
c_prime[0] = c[0] / b[0]
d_prime[0] = d[0] / b[0]
for i in range(1, n-1):
denominator = b[i] - a[i] * c_prime[i-1]
c_prime[i] = c[i] / denominator
d_prime[i] = (d[i] - a[i] * d_prime[i-1]) / denominator
d_prime[n-1] = (d[n-1] - a[n-1] * d_prime[n-2]) / (b[n-1] - a[n-1] * c_prime[n-2])
x = np.zeros(n)
x[n-1] = d_prime[n-1]
for i in range(n-2, -1, -1):
x[i] = d_prime[i] - c_prime[i] * x[i+1]
return x
def pricing(sigma, r, Tmax, K, N, M, E, X, t,Amax):
delta_t = (Tmax) / E
A = np.linspace(0,Amax, M+1)
h_S = np.zeros(N+1)
h_A = np.zeros(M+1)
V = np.zeros(shape=(E+1, N+1, M+1))
V_half = np.zeros((N+1, M+1)) # Matrice pour stocker V^{n+1/2}
# Initialization of S[i] and h_S[i].
S = np.zeros(N+1)
h = X / (1 + ((sigma**2)/r) * (N-1))
for i in range(1, N+1):
if i == 1:
S[i] = h_S[i] = h
else:
S[i] = h * (1 + (sigma**2)* (i-1)/r)
h_S[i] = h * (sigma**2) / r
for j in range(0, M+1):
h_A[j] = Amax / M
for i in range(1,N+1):
for j in range(0,M):
V[E][i][j] = max(A[j]/Tmax - K,0) # Terminal condition
Time loop for solving with the ADI scheme.
for n in range(E-1, -1, -1):
#First ADI sub-step (implicitly in S)
for j in range(0, M): #
a = np.zeros(N-1)
b = np.zeros(N-1)
c = np.zeros(N-1)
d = np.zeros(N-1)
for i in range(1, N):
hi = h_S[i]
hi_1 = h_S[i+1]
a[i-1] = (delta_t*(-(sigma**2) * S[i]**2) / ((hi + hi_1) * hi) + r * S[i]*delta_t / (hi + hi_1))
b[i-1] = (delta_t*((sigma**2) * S[i]**2) / (hi*hi_1) + r*delta_t +1)
c[i-1] = (delta_t*(-(sigma**2) * S[i]**2) / ((hi + hi_1) * hi_1) - r * S[i]*delta_t / (hi + hi_1))
d[i-1] = V[n+1][i][j]
V_half[0, j] = exp(-r * (Tmax - n*delta_t)) * max((A[j] / Tmax - K), 0) # sera toujours nul pour A<KT
V_half[N, j] = (X / (r * Tmax)) * (1 - exp(-r * (Tmax - n*delta_t))) + exp(-r * (Tmax - n*delta_t)) * ((A[j] / Tmax) - K)
V_half[1:N, j] = thomas_algorithm(a, b, c, d)
for i in range(1, N+1):
a = np.zeros(M)
b = np.zeros(M)
c = np.zeros(M)
d = np.zeros(M)
for j in range(0, M):
h_A_j1 = h_A[j]
a[j-1] = 0
b[j-1] = (delta_t*S[i] / h_A_j1) +1
c[j-1] = -delta_t*S[i] / h_A_j1
d[j-1] =V_half[i, j]
if A[j]>=K*Tmax :
V[n][i][j] = (1 - exp(-r * (Tmax - n*delta_t))) * (S[i] / (r * Tmax)) + (A[j]/Tmax - K)*exp(-r * (Tmax - n*delta_t))
V[n, i, 0:M] = thomas_algorithm(a, b, c, d)
return VA = np.linspace(0,K*Tmax,M+1)
S = np.linspace(0,X,N+1)
X, Y = np.meshgrid(S, A)
V = pricing_test_end(sigma=0.4, r=0.06, Tmax=1, K=2, N=30,M=30, E=10, X=8 ,t=0.5,Amax=6)[5][:][:]
ax = plt.axes(projection='3d')
ax.plot_surface(X,Y, V,cmap='viridis')
# Nommer les axes
ax.set_xlabel('Prix de A')
ax.set_ylabel('Prix du sous-jacent (S)')
ax.set_zlabel('Prix de l\'option (V)')
plt.legend()
Thanks,
Attachments
Last edited: