interesting problem

[shikamaru]

Triangle ABC has sides of length 45, 60, and 75. Place a point D randomly and uniformly inside the triangle. What is the expected value of the sum of perpendicular distances from point D to the triangle's three sides?

 

[Rajan Seth]

Is the answer 37.5?

 

[shikamaru]

i don't know solution,can you post here?

 

[Pavlos Sakoglou]

52.5

 

[TheComplexUnit]

The triangle is right-angled, say, with vertices (0,0), (60,0) and (0,45). A quick MC simulation suggests that the sum of the perpendicular distances is around 47.

 

[Pavlos Sakoglou]

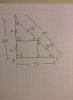
I solved it suggesting that the point D could also be a tagent point to the hypotenuse of the triangle with two perpendicular distances. That way if the D point is placed right in the middle of the hypotenuse (segment BC) then it should intersect in the middle the other two segments. See my attached drawing so to understand my thinking.

 

[TheComplexUnit]

I solved it suggesting that the point D could also be a tagent point to the hypotenuse of the triangle with two perpendicular distances. That way if the D point is placed right in the middle of the hypotenuse (segment BC) then it should intersect in the middle the other two segments. See my attached drawing so to understand my thinking.

Hmm, 52.5 is obviously right insofar as D is restricted to lie on the hypotenuse. This, however is not how the problem is formulated (you must tell me why you think your solution generalises to the "internal region" of the triangle).

 

[Rajan Seth]

I think 47 is right, this is how I proved it.
The lengths are 45, 60 and 75.
For clarity sake lets take
3,4 and 5 and then we will scale our answer by 15.

Let the coordinate of the triangle be
(0,0) (3,0) and (0,4)

Equation of Hypotenuses becomes (x/3 + y/4 -1 = 0)

Now any point (x,y) in the triangle would have perpendicular distance from side as

x + y + (12/5 - 0.8x - 0.6x) = 2.4 + 0.2x + 0.4y

distance from x axis + distance from y axis + distance from Hypotenuses

The answer would be expected value of above

2.4 + 0.2[x] + 0.4[y]

[x] in triangle = x co ordinate of centroid = 1
[y] = y co ordinate of centroid = 4/3

substituting the values ans scaling to 15

(2.4 + 0.2 + 1.6/3)15

= 39 + 8
=47

 

[shikamaru]

i don't think so,because D(x,y) randomly and uniformly inside the triangle,x and y has relationship as x/3+y/4<1,

I think 47 is right, this is how I proved it.
The lengths are 45, 60 and 75.
For clarity sake lets take
3,4 and 5 and then we will scale our answer by 15.

Let the coordinate of the triangle be
(0,0) (3,0) and (0,4)

Equation of Hypotenuses becomes (x/3 + y/4 -1 = 0)

Now any point (x,y) in the triangle would have perpendicular distance from side as
x + y + (12/5 - 0.8x - 0.6x) = 2.4 + 0.2x + 0.4y

distance from x axis + distance from y axis + distance from Hypotenuses

The answer would be expected value of above

2.4 + 0.2[x] + 0.4[y]

[x] in triangle = x co ordinate of centroid = 1
[y] = y co ordinate of centroid = 4/3

substituting the values ans scaling to 15

(2.4 + 0.2 + 1.6/3)15

= 39 + 8
=47

 

[Rajan Seth]

i don't think so,because D(x,y) randomly and uniformly inside the triangle,x and y has relationship as x/3+y/4<1,

0<x<3
0<y<4
x/3 + y<4 -1 < 0

I understand this is the condition and therefore [x] and [y] is not 1.5 and 2.

All the 3 equation represent the triangle and [x] and [y] is centroid (x1+x2+x3)/3 and (y1+y2+y3)/3
You can simulate x and y "randomly and uniformly " with the above condition to check for correctness

 

[shikamaru]

Can you explain why [x]=1 [y]=4/3?
Thank you very much

 

[Rajan Seth]

Can you explain why [x]=1 [y]=4/3?
Thank you very much

Doing it the hard way. This should be good

 

[Pavlos Sakoglou]

Doing it the hard way. This should be good

View attachment 9808

either I am really bad with geometry, either you brought it to a new level smart.

 

[atq]

I made a video on this problem a while ago .
Hope you'll find it useful, as there are quite a few different answers in this thread!

 

[ptf]

The correct answer is 47

 

[radosr]

Nice problem!
The distance from a point with coordinates (x,y) to a given side is a linear function of the coordinates x and y; so, the sum of the distances to the three sides is also linear in x and y. Using linearity of expectation, the expected value is then the average of the values when the point is in one of three corners of the triangle; in other words, the average of the three altitudes of the triangle. Since the altitudes are 36, 45, and 60, the expected value is their average, which is 47.

 

[ptf]

The correct answer is 47

 

[ptf]

I made a video on this problem a while ago .
Hope you'll find it useful, as there are quite a few different answers in this thread!

 

[atq]

Let's start from the beginning. Here is a simple code that does the computes the same estimate as you do:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
np.random.seed(42)

x_length = 60
y_length = 45

N = int(1e6)

def get_estimate(N, x_length, y_length):
    x_values = np.random.rand(N)*x_length
    y_values = np.random.rand(N)*y_length

    colors = ["RED" if y_values[n]<= -y_length/x_length*x_values[n] + y_length \
        else "BLUE"  for n in range(len(x_values))]
    
    figure(figsize=(16, 12), dpi=200)
    plt.scatter(x_values, y_values, c=colors, s=1e4/N)
    plt.title(f"N={N}")
    plt.show()
    
    dists=[]
    for n in range(N):
        if y_values[n]<= -y_length/x_length*x_values[n] + y_length:
            dists.append(36+2/5*x_values[n] + 1/5*y_values[n])
    
    print(f"Simulated sum of distances: {np.mean(dists)}")

First round, with 10000 simulations(RED points inside the triangle, for which we compute the sum of distances; BLUE points outside the triangle, for which we do nothing)

Simulated sum of distances: 46.99828952360751
Second round, with 100000 simulations:

Simulated sum of distances: 47.01289711967379
Third round, with 1000000 simulations:
Simulated sum of distances: 46.99724786291175

You can also use a very similar code to check that the expected value of X is indeed 20, not 30.

Even if we were to consider that X~U(0,60), do you also imply that Y~U(0,45)? In this case, and following your logic, E[2X+Y] = 82.5, which gives an expected sum of distances of 52.5;

 

[ptf]

Let's start from the beginning. Here is a simple code that does the computes the same estimate as you do:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
np.random.seed(42)

x_length = 60
y_length = 45

N = int(1e6)

def get_estimate(N, x_length, y_length):
    x_values = np.random.rand(N)*x_length
    y_values = np.random.rand(N)*y_length

    colors = ["RED" if y_values[n]<= -y_length/x_length*x_values[n] + y_length \
        else "BLUE"  for n in range(len(x_values))]
   
    figure(figsize=(16, 12), dpi=200)
    plt.scatter(x_values, y_values, c=colors, s=1e4/N)
    plt.title(f"N={N}")
    plt.show()
   
    dists=[]
    for n in range(N):
        if y_values[n]<= -y_length/x_length*x_values[n] + y_length:
            dists.append(36+2/5*x_values[n] + 1/5*y_values[n])
   
    print(f"Simulated sum of distances: {np.mean(dists)}")

First round, with 10000 simulations(RED points inside the triangle, for which we compute the sum of distances; BLUE points outside the triangle, for which we do nothing)
View attachment 40478
Simulated sum of distances: 46.99828952360751
Second round, with 100000 simulations:
View attachment 40479
Simulated sum of distances: 47.01289711967379
Third round, with 1000000 simulations:
Simulated sum of distances: 46.99724786291175

You can also use a very similar code to check that the expected value of X is indeed 20, not 30.

Even if we were to consider that X~U(0,60), do you also imply that Y~U(0,45)? In this case, and following your logic, E[2X+Y] = 82.5, which gives an expected sum of distances of 52.5;

I just think about it again. You are right. My method made a mistake where I see X as uniform but it's not.