the answer is 28 meters is the distance expected to be covered in 10 walks under the prescription that every time you walk at 45 degrees to top point of the wall and 45 degrees in towards the B point. this makes a distance of 2.82 meters per walk. and for 10 walks it will be 28.2 meters. if you go by probability then minimum distance is 20 meters and the maximum distance is 40 meters. it could be anywhere in between if you hit the wall every time and then move alone the wall, so wall or no wall, follow the 45 degree path and you will make 2.82 meters distance per walk and for 10 walks 28.2 meter
contact me on
jawadwaheed09@gmail.com
The question asks for total distance after 10 walks and coin flips. You are saying that 2*sqrt(2) is the minimal distance one should cover for each walk, regardless of a wall blocking your path or not.
Since a fair-sided coin implies that half of our walks will NOT have a wall, it is wasteful to walk the extra distance. So instead, we are tasked to find a height (call it H) on the wall that will minimize the distance walked while also taking into account the possibility of a wall blocking our path.
The points H, A (or B, depending on orientation) and O (the point where the wall intersect distance between point A and B) form a right triangle, with base = distance between point A (or B) and O = 1 , height = H. Using Pythagoras' theorem,
Hypotenuse = distance we walk to the wall from A or B = Sqrt(1+H^2)
Now, consider these two cases:
1. (Worst case) There is a wall: We must now walk an additional 1-H meters to the top of the wall, and another Sqrt(2) meters from the top of the wall to our endpoint. The distance covered by walking this case is given by the function f:
f(H) = sqrt(1+H^2) + (1-H) + Sqrt(2)
2. (Best case) There is no wall: We need only walk Sqrt(1+H^2) meters to our endpoint. The distance covered by walking this case is given by the function g:
g(H) = 2*sqrt(1+H^2)
So ultimately,we want a find an H large enough to ensure that our additional 1-H meters in our worst case is small, but we also need H small enough so that our distance covered in the best case is minimal. In other words, we want a value of H that will optimally minimize both functions.
Given that a fair-sided coin is flipped each time we walk from point A or B, it is safe to assume that 5 of these walks will have walls and 5 will not. From this, we can determine the total distance covered over 10 walks, which will be the function d:
d(H) = 5*f(H)+5*g(H) = 5*(sqrt(1+H^2) + (1-H) + Sqrt(2)) + 5*(2*Sqrt(1+H^2))
Minimizing d(H) is essentially the same as finding the optimal H that minimizes f(H) and g(H)
simultaneously.
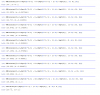
Minimizing d(H), we see that the minimal total distance covered is 26.2132 meters from the height H = 0.353553 meters.
Also: it is worth noting that this H will change with respect to the probability of the coin tosses. For example, if there was a 60% chance of heads,, or a 60% chance of a wall, then we would have 6 worst case scenarios and 4 best case scenarios: in this instance, H= 0.474342 for a total distance of 27.1344 meters.
The picture I'm including considers various outcomes for coin tosses and their impact on H